
Table of Contents
Future Motion Dynamic Modeling via Hybrid Supervision for Multi-Person Motion Prediction Uncertainty Reduction Link to Future Motion Dynamic Modeling via Hybrid Supervision for Multi-Person Motion Prediction Uncertainty Reduction
https://dl.acm.org/doi/10.1145/3664647.3681528
Abstract Link to Abstract
多人运动预测由于运动动态的复杂性以及个体间交互的多样性而始终是一项具有挑战性的问题,且随着预测时间范围的延长,不确定性会快速增加。
现有方法往往忽略预测帧之间的运动动态建模,将其完全交由深度神经网络处理,使模型缺乏动态归纳偏置,从而导致性能欠佳。
本文提出了一种高效的多人运动预测方法,称为 (Hybrid Supervision Transformer),该方法将预测区间内的动态建模构建为一种新颖的混合监督任务。
具体而言,我们的方法执行一种滚动预测过程,并引入混合监督机制,使模型能够基于(通常包含误差的)先前预测来预测后续帧的姿态。
除了标准监督损失外,我们进一步引入了两种自监督与辅助监督机制,它们分别最小化使用含误差输入得到的预测与使用无误差(真实值)输入得到的预测之间的距离,并指导模型基于真实值进行精确预测,从而分别提升模型对推理阶段输入偏差的鲁棒性并稳定训练过程。
同时,我们将 等优化技术引入模型以提高训练效率。
此外,我们设计了一个细粒度时空相关性捕获模块,用于辅助特征学习并减少由于个体之间复杂多变的交互所导致的不确定性。
我们的方法在多个多人数据集的短期和长期预测任务中均取得了当前最先进的结果。
Introduction Link to Introduction
挑战性:预测时间范围内显著的运动动态不确定性,即需要预测的未来步长本身高度不稳定。
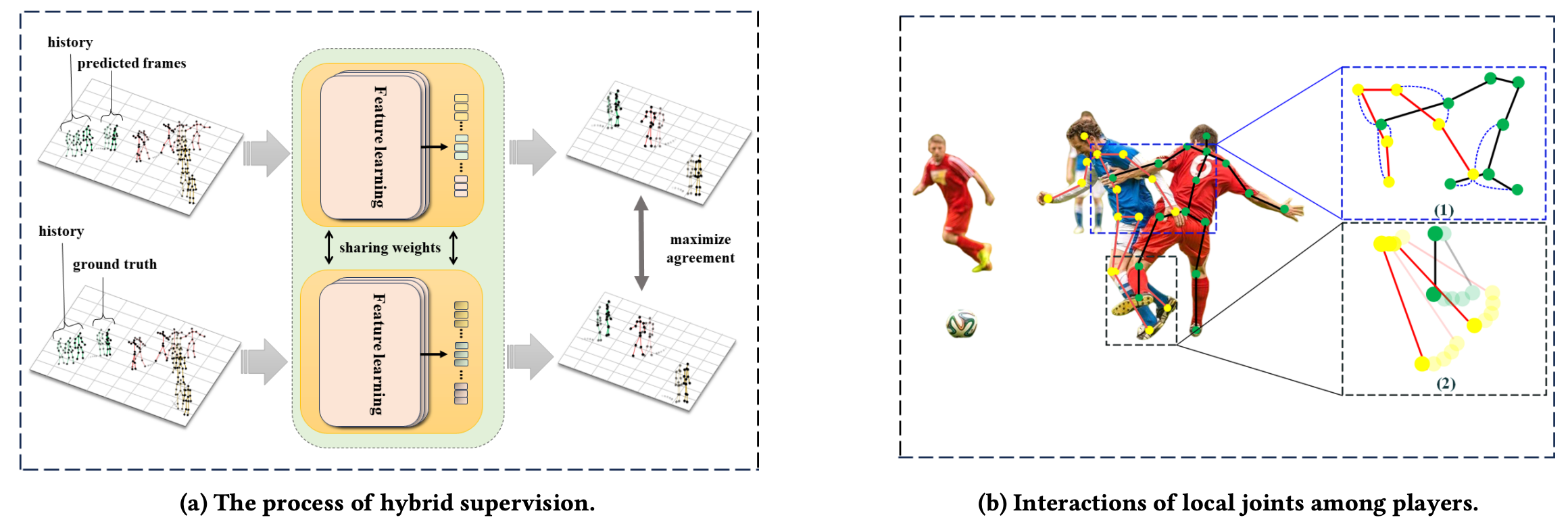
不确定性主要来源于两个方面:
其一,个体之间复杂多变的交互。
例如,图 1b (1) 显示红色玩家的左手腕关节会遮挡蓝色玩家躯干区域的多个关节,而蓝色玩家的左手腕关节又会遮挡红色玩家的髋关节。
其二,人类运动的演化模式本身较为复杂。
例如,不同关键点的运动特性差异很大,如图 1b (2) 所示,玩家膝关节的运动范围远小于脚踝关节。
这些不确定性会随着预测时间范围的增加而迅速增长。
在预测时间范围内显式建模运动动态应是一个不可或缺的模块,以减少不确定性并最终提升运动预测的准确性,但这一点在以往研究中往往被忽视,它们通常完全依赖解码器神经网络来处理这一问题。
为了解决上述问题,我们提出了一种新的基于 Transformer 的框架 Hybrid Supervision Transformer(HSFormer)。
我们的核心思想是在预测时间范围内通过构建相邻帧之间的依赖关系来显式建模运动动态。
首先,我们提出一种滚动预测过程,该过程通过(通常包含误差的)先前预测来预测下一帧的姿态。
在使用普通优化算法时,模型可能会受到上一轮==预测累积误差==的干扰。
因此,除了标准监督损失(最小化真实值与滚动预测输出之间的距离)之外,引入了两种额外的监督机制:
- 自监督:最小化带误差输入的预测与无误差(真实值)输入的预测之间的距离
- 辅助监督:引导模型基于真实值进行准确预测
标准监督、自监督与辅助监督共同构成了我们提出的混合监督训练框架。
同时,我们还将 stop-gradient 和参数共享等额外优化技术扩展到 HSFormer 以提升训练效率。
此外,为了减少由复杂交互带来的不确定性,HSFormer 引入了一个特征学习组件——时空编码器(Spatio-Temporal Encoder, STE)模块,用于更细致的建模。
STE 包含两个子模块:
- 空间关节编码器(Spatial Joint Encoder, SJE):捕获单帧内部关节之间的关系
- 时间关节编码器(Temporal Joint Encoder, TJE):捕获关节在时间维度上的动态变化
3 Preliminaries Link to 3 Preliminaries
3.1 Problem Formulation Link to 3.1 Problem Formulation
给定多人的历史运动轨迹,我们的目标是预测这些人的未来运动。形式化地,假设场景中有 个个体,第 个个体包含 个时间步的历史运动轨迹,可表示为:
其中每个 ,表示包含 个骨架关节的三维坐标。
将 转换为:
通过计算相邻项之间的差分,使模型更容易捕捉运动趋势,即:
我们的目标是预测未来 帧的三维姿态序列,即:并将其转换回:
其中 。
3.2 Pipeline Link to 3.2 Pipeline
给定一个三维姿态序列:,其中包含 个个体, 个关节,输入长度为 。
基础 pipeline
- 首先对运动序列应用离散余弦变换(Discrete Cosine Transformation,DCT),将其编码到频率域中,从而得到更紧凑的表示。
- 然后,该表示被映射到高维特征空间以获得嵌入特征:,其中 为特征维度。
- 随后, 被送入编码器以学习序列特征,然后通过解码器预测未来序列。
- 最后,pipeline 使用全连接层(FC)以及逆离散余弦变换(IDCT)生成未来预测:
在本文中,我们重新设计了编码器和解码器,以减少预测不确定性,这是本文的核心贡献。
具体而言,我们提出如下两个模块:
• Fine-grained Correlation Learning(见第 4 节) Link to • Fine-grained Correlation Learning(见第 4 节)
我们提出了一个时空编码器(Spatio-Temporal Encoder, STE),用于实现细粒度特征学习,以减少源自个体间复杂和多变交互的预测不确定性。
STE 能够学习:
- 每一帧内部关节之间的关系
- 不同帧之间各关节的全局时间相关性
• Dynamic Modeling via Hybrid Supervision(见第 5 节) Link to • Dynamic Modeling via Hybrid Supervision(见第 5 节)
我们提出一种滚动预测方案,以显式学习相邻帧运动之间的依赖关系。
此外,我们设计了一个新的混合监督机制,以保证:
- 训练效率
- 模型的鲁棒性,避免预测误差累积
从而提高整体预测性能。
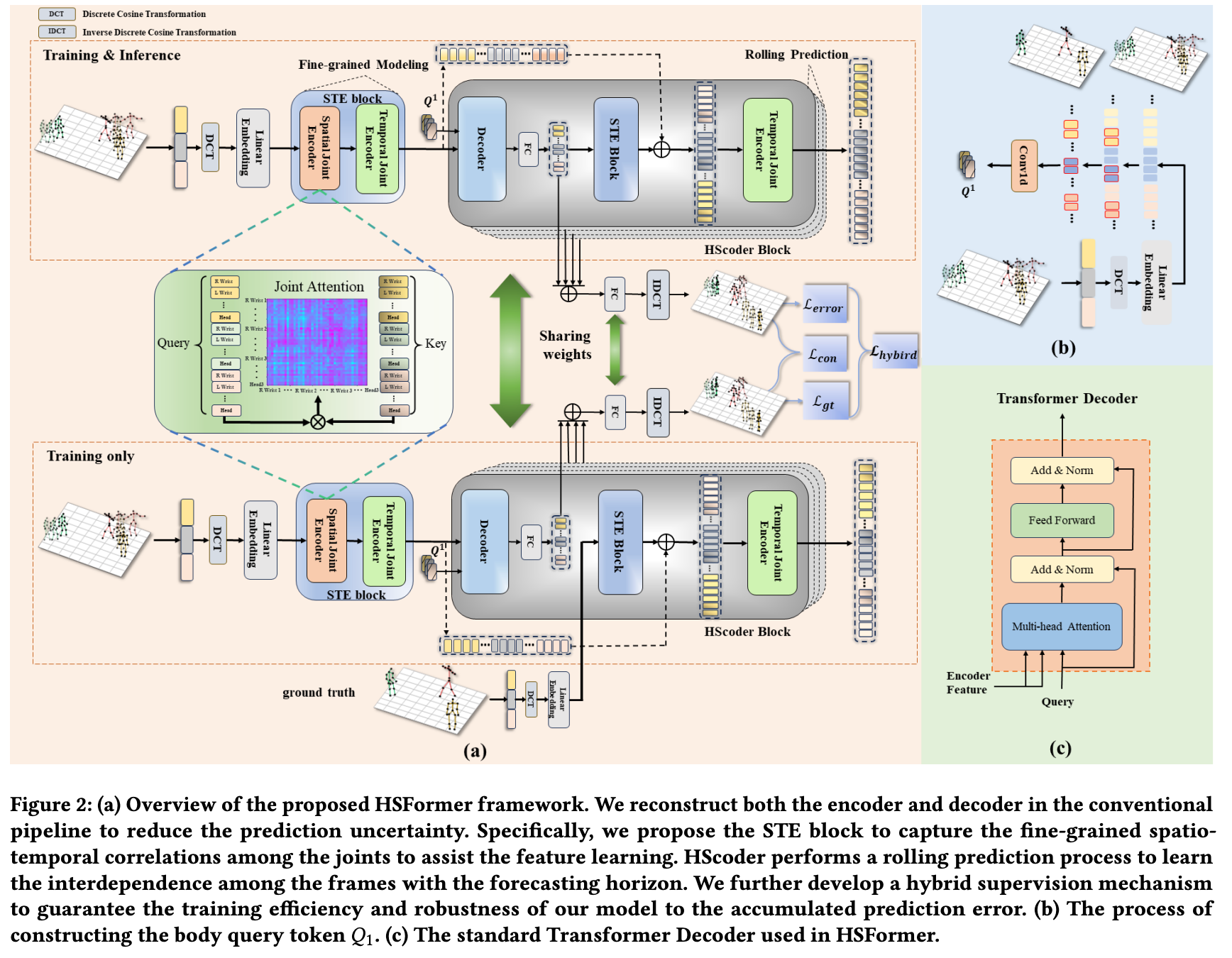
4 Fine-grained Correlation Learning Link to 4 Fine-grained Correlation Learning
为了便于介绍我们的方法 HSFormer,我们首先引入细粒度相关性学习模块 STE,因为它被集成在编码器和解码器两个部分中。
STE 模块旨在辅助特征学习,以减少来自个体间复杂且多变交互带来的不确定性。如图 2 所示,STE 包含一个 SJE 模块和一个 TJE 模块,它们分别学习:
- 每一帧内部的关节关系
- 跨帧的全局时间相关性
Spatial Correlation Learning Link to Spatial Correlation Learning
SJE 的目标是通过注意力机制学习所有个体的跨关节空间关系。
假设 SJE 模块包含 层,我们将嵌入特征 与可学习的位置嵌入:相结合,并在 SJE 的第一层之前构造出嵌入特征:
SJE 模块接收来自同一帧的 个 token(每个 token 维度为 ),并建模跨关节的关系。完成后,token 将包含同一帧内其他个体关节的信息。
最终一层的输出可以表示为:

Temporal Correlation Learning Link to Temporal Correlation Learning
由于关节运动的多样性,学习每个关节的独立运动特征至关重要。TJE 模块将每个关节的运动轨迹视为一个独立单元,从而能够识别每个关节独特的运动模式。
我们首先将 SJE 的输出特征: reshape 为:
然后与可学习的时间位置编码:相结合,得到:
随后, 被送入 TJE 模块,以并行学习每个关节的时间依赖性。
在经过 TJE 模块处理后,最终输出为:,其中 为 TJE 的层数。
5 Dynamic Modeling via Hybrid Supervision Link to 5 Dynamic Modeling via Hybrid Supervision
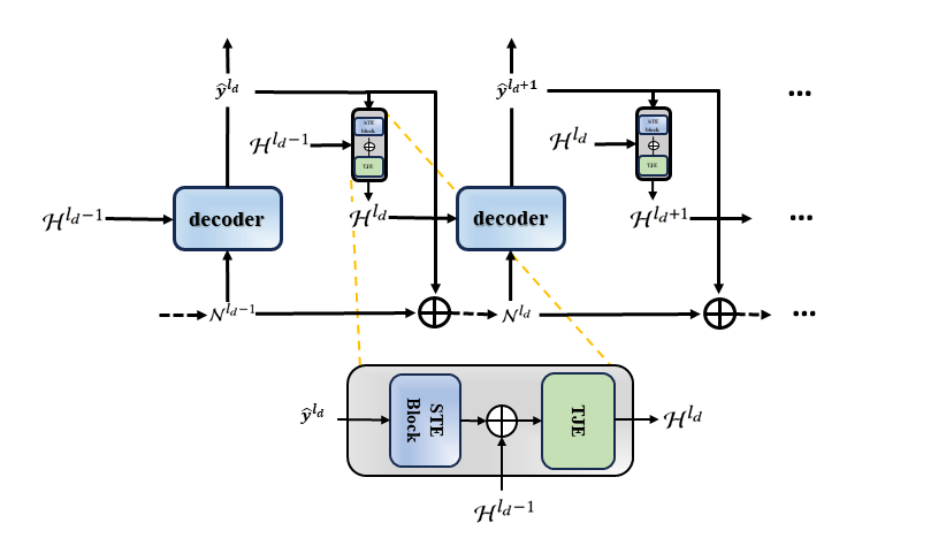
5.1 Rolling Prediction Scheme Link to 5.1 Rolling Prediction Scheme
我们重构了解码器部分(称为 HScoder block),该模块旨在通过滚动预测过程学习未来帧的动态,以减少不确定性。
如图 3 所示,这一过程会将预测区间划分为多个子区间,并依次预测运动。
设划分区间的长度为 ,则滚动预测一共包含:轮预测。
对于第 轮(),HScoder 首先基于最近 帧的邻域运动动态构造 body query token:
其中邻域动态表示为:
计算方式为:Q^{l_d} = \text{Conv1d}(\mathcal{N}^{\,l_d}) \tag{1}
其中 是卷积核大小为 的一维卷积。
随后,HScoder 使用 Transformer Decoder 预测未来 帧的 pose 特征:
基于 以及历史上下文 ,公式为:\hat{y}^{\,l_d} = \text{FC}(\text{Decoder}(Q^{l_d}, H^{l_d})) \tag{2}
其中 FC 是将单个 token 转换为 帧的线性层。
我们的滚动预测方案利用 与 分别获取:
- 初始邻域运动动态
- 初始历史上下文
然后利用上一轮预测结果 与已有的 和 构建新的邻域动态与历史上下文,具体为:
邻域动态更新: Link to 邻域动态更新:
\mathcal{N}^{\,l_d} = \begin{cases} \text{Slice}(\mathcal{F}_{\text{Embed}}), & l_d = 1 \\[4pt] \text{Slice}(\text{Concat}(\mathcal{N}^{l_d-1}, \hat{y}^{\,l_d-1})), & l_d > 1 \end{cases} \tag{3}
其中 用于获取最近 帧特征。
历史上下文更新: Link to 历史上下文更新:
首先将预测结果 重新编码到历史上下文的特征空间:\hat{z}^{\,l_d} = \text{STE}(\hat{y}^{\,l_d}) \tag{4}
随后,TJE 提取上下文间的时间依赖性:
H^{\,l_d} = \begin{cases} \mathcal{F}^{L_2}_{\text{TJE}}, & l_d = 1 \\[4pt] \text{TJE}(\text{Concat}(H^{l_d-1}, \hat{z}^{\,l_d-1})), & l_d > 1 \end{cases} \tag{5}
其中:
经过 次滚动预测后,我们将所有预测特征 拼接并投影生成最终的预测 pose 序列:
\hat{Y}_{T+1:T+F} = \text{IDCT}\left( \text{FC}\left( \text{Concat}(\hat{y}^{1}, \hat{y}^{2}, \ldots, \hat{y}^{d}) \right) \right) \tag{6}
最终, 将被转回为 。
5.2 Hybrid Supervision Mechanism Link to 5.2 Hybrid Supervision Mechanism
在滚动预测框架下训练网络并不容易,因为前一轮预测的误差会逐步累积,影响后续预测,尤其在早期训练阶段容易导致训练失败。
为解决这一问题,我们提出:
- 一个 gt-augment 分支
- 一个混合监督机制
gt-augment 分支提供一条不会受到预测误差累积影响的更稳定的优化路径,增强训练稳定性。
gt-augmented 分支 Link to gt-augmented 分支
该分支仅在训练中使用,推理时会移除。
它与主分支共享相同架构和权重,但使用 真实值而非上一轮预测值 作为输入。
在第 轮中,它将 Eq. (3)(4) 中的预测特征 替换为来自真实值的特征:
[y^{1}_{gt}, \ldots, y^{l_d}_{gt}, \ldots, y^{d}_{gt}] = \text{FC}(\text{DCT}(Y_{T+1:T+F})) \tag{7}
Loss Functions Link to Loss Functions
设真实值为 ,主分支输出为 ,gt 分支输出为 。
定义 MSE 损失为:
我们训练一个双分支模型,包含以下三种监督机制:
1. Standard Supervision Link to 1. Standard Supervision
强制模型在输入含误差的预测时也能做出准确预测:
2. Auxiliary Supervision Link to 2. Auxiliary Supervision
避免早期训练阶段因误差累积导致训练失败,通过真实姿态监督模型:
3. Self Supervision Link to 3. Self Supervision
引入对比式自监督损失,最小化含误差输入与无误差输入预测之间的差异:
其中 为 stop-gradient 操作。
Overall Loss Link to Overall Loss
综合损失为:
\mathcal{L}_{\text{hybrid}} = \lambda \mathcal{L}_{\text{error}}+(1 - \lambda) \mathcal{L}_{gt}+\gamma \mathcal{L}_{con} \tag{8}
其中:
- 用于平衡不同损失
- 调整自监督损失权重
实验中 均能获得良好效果。
为稳定训练过程:
- 初期使用较小的 (更依赖 gt 分支)
- 随训练逐渐将 增大到 1(完全依赖主分支)
从而保证训练与推理过程一致。