LongCat-Video Technical Report Link to LongCat-Video Technical Report

https://arxiv.org/abs/2510.22200

https://huggingface.co/papers/2510.22200

一、Model Architecture Link to 一、Model Architecture

WAN2.1 VAE：（时间，高度，宽度）4×8×8压缩比

DiT模型中的分块操作进一步将潜在变量压缩，额外压缩比为1×2×2

因此，从像素到潜在变量的整体压缩比达到4×16×16

二、Block Attention With KV Cache Link to 二、Block Attention With KV Cache

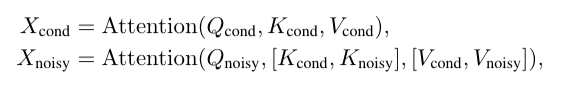
• 公式（1）： 条件帧的注意力计算 仅依赖自身 —— 条件帧的查询 $Q_{\text{cond}}$、键 $K_{\text{cond}}$、值 $V_{\text{cond}}$ 均来自 $X_{\text{cond}}$，不与待去噪帧的键 / 值交互。

  目的：确保条件帧的内容（如 Image-to-Video 的参考图像、Video-Continuation 的已有帧）不被待去噪帧的噪声干扰，维持生成的基础逻辑稳定。

• 公式（2）： 待去噪帧的注意力计算 依赖自身 + 条件帧 —— 待去噪帧的查询 $Q_{\text{noisy}}$ 会同时关注 “条件帧的键值 $(K_{\text{cond}}, V_{\text{cond}})$” 和 “自身的键值 $(K_{\text{noisy}}, V_{\text{noisy}})$”。

  目的：让待去噪帧（生成帧）学习条件帧的内容逻辑，例如在 Video-Continuation 中，后续生成的 50 帧会参考前 10 帧的人物动作、场景光影，确保时序连贯。

在长视频生成中，条件帧的数量可能很多，若每次采样都重新计算条件帧的键值 $(K_{\text{cond}}, V_{\text{cond}})$，会造成大量重复计算

• 缓存逻辑： 条件帧的 $K_{\text{cond}}$ 和 $V_{\text{cond}}$ 仅在第一次计算后缓存到内存中，后续所有采样步骤（如续播多段帧）直接复用缓存结果；
• 优势： 既确保训练与推理过程中条件帧的一致性，又大幅减少长视频生成的计算量，提升推理效率。

三、Efficent Video Generation Link to 三、Efficent Video Generation

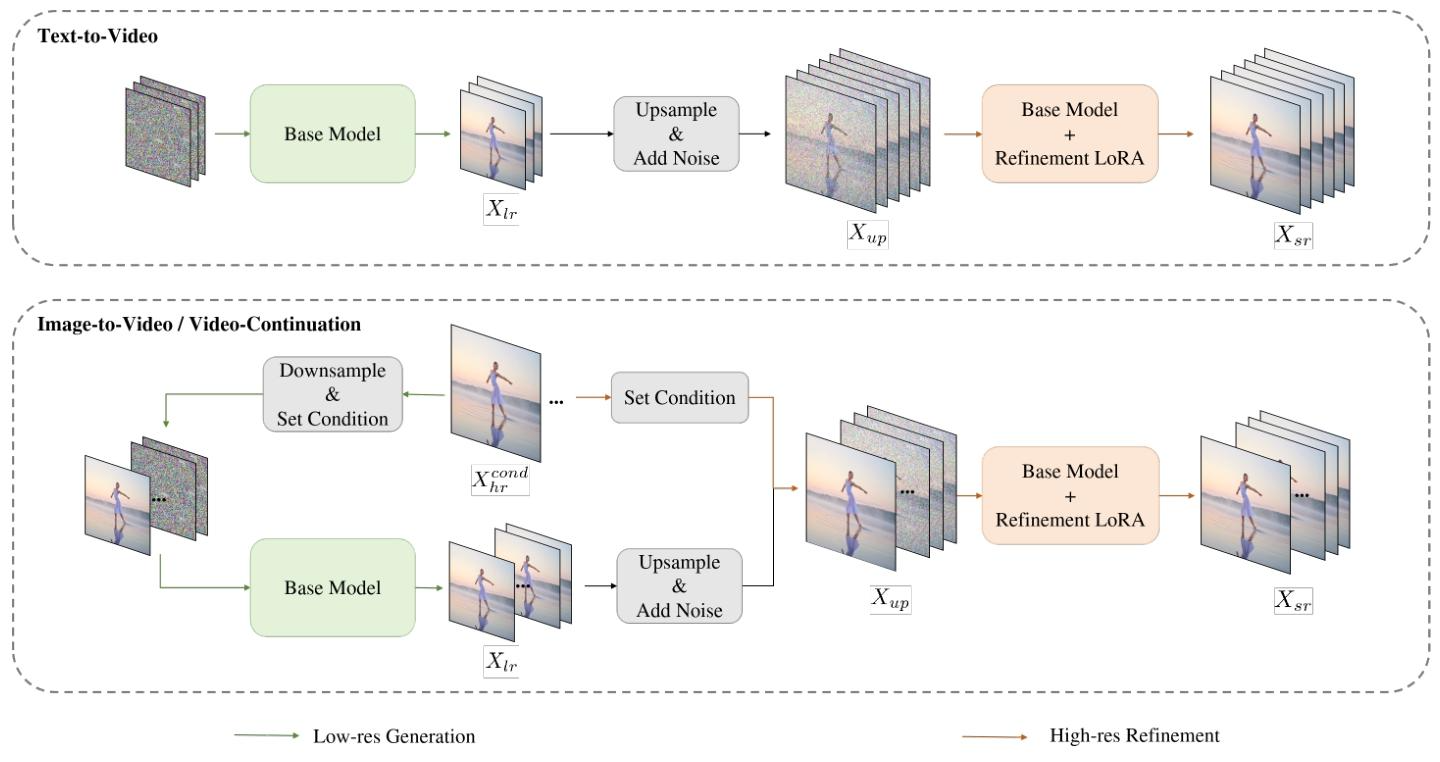
1. Coarse-to-Fine Generation Link to 1. Coarse-to-Fine Generation

第一阶段：生成低分辨率（LR）基础视频 Link to 第一阶段：生成低分辨率（LR）基础视频

1. 目标： 快速搭建视频的“结构框架”，包括场景布局、人物动作轨迹、时序逻辑；
2. 配置： 生成 480p、15fps 的视频，采样步数 16 步（蒸馏后），确保快速出结果；
3. 核心： 不追求细节，重点保证结构完整、时序连贯，为后续优化打基础。

第二阶段：高分辨率（HR）优化与帧率提升 Link to 第二阶段：高分辨率（HR）优化与帧率提升

1. 上采样预处理： 用三线性插值将 480p、15fps 视频放大至 720p、30fps，保留基础结构，但此时画面会有模糊、纹理缺失等问题；
2. 优化专家训练： 训练专门的“精细化专家 LoRA 模块”，基于基础模型微调，专注于“修正模糊、补充细节、提升帧率一致性”；
3. 流匹配建模： 用流匹配算法建模“上采样低质视频”与“目标高质视频”的分布映射，具体逻辑：
   • 输入：上采样后的视频 latent $(x_{\text{up}})$ + 适度噪声 $(t_{\text{thresh}} = 0.5)$，避免过度修改基础结构；
   • 目标：学习从“带噪上采样视频”到“720p、30fps 高质视频”的平滑过渡，仅需 5 步采样；
   • 数值约束：对 velocity（速度场）进行数值缩放，确保与基础模型的数值范围一致，保证生成连贯性。

2.Block Sparse Attention Link to 2.Block Sparse Attention

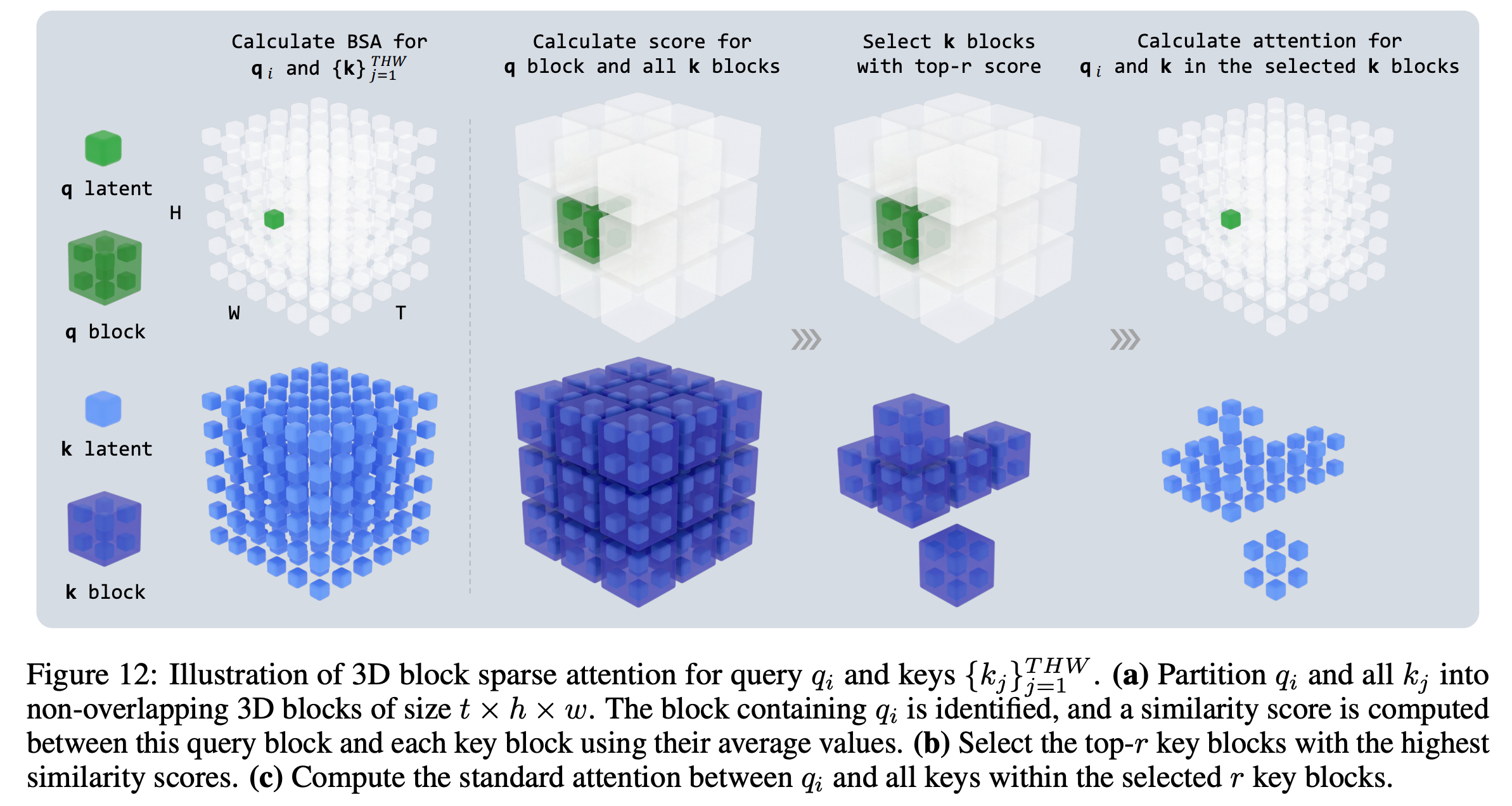
（1）块稀疏注意力（Block Sparse Attention）的建模 Link to （1）块稀疏注意力（Block Sparse Attention）的建模

• 3D 块重排（3D Block Rearrangement）

  我们考虑一个形状为 $T \times H \times W$ 的视频序列，其在内存中的存储顺序为 $(T, H, W)$。

  该序列被划分为 $N_T \times N_H \times N_W$ 个三维块（3D blocks），其中 $N_T = \lceil T / t \rceil$, $N_H = \lceil H / h \rceil$, $N_W = \lceil W / w \rceil$，

  每个块的形状为 $t \times h \times w$。

  这些块在内存中的排列顺序为 $[N_T, N_H, N_W]$（块级顺序）， 并且在每个块内，元素按 $[t, h, w]$（块内顺序）排列。

  经过这种重排后，我们得到一个重新排序的序列。

• 块选择掩码的构建（Block Selection Mask Construction）

  设 $X$ 为重排后的输入张量。

  我们使用可学习的权重矩阵 $W_q$ 和 $W_k$ 来计算查询（query）矩阵 $Q$ 和键（key）矩阵 $K$：

  $Q = XW_q \in \mathbb{R}^{b \times n_h \times s_q \times d}, \quad K = XW_k \in \mathbb{R}^{b \times n_h \times s_k \times d},$

  其中 $b$ 是批量大小（batch size），$n_h$ 是注意力头（attention heads）的数量， $s_q$ 和 $s_k$ 分别是查询和键的序列长度（在本例中 $s_q = s_k = T \times H \times W$）， $d$ 是特征维度（feature dimension）。

  为降低计算成本，我们在每个块内执行平均池化（average pooling）。

  设 $n = t \times h \times w$ 为每个块的元素数。

  池化后的查询 $Q_{\text{pool}}$ 和键 $K_{\text{pool}}$ 定义为：

  $Q_{\text{pool}}[:, :, b_q, :] = \frac{1}{n} \sum_{j=0}^{n-1} Q[:, :, (b_q - 1)n + j, :], \quad b_q = 1, \ldots, N_q,$

  $K_{\text{pool}}[:, :, b_k, :] = \frac{1}{n} \sum_{j=0}^{n-1} K[:, :, (b_k - 1)n + j, :], \quad b_k = 1, \ldots, N_k,$

  其中 $N_q = s_q / n$，$N_k = s_k / n$，分别表示查询块与键块的数量。

  池化后的得分矩阵 $S_{\text{pool}}$ 计算如下：$S_{\text{pool}} = \frac{Q_{\text{pool}} K_{\text{pool}}^{\top}}{\sqrt{d}} \in \mathbb{R}^{b \times n_h \times N_q \times N_k},$

  其中 $K_{\text{pool}}^{\top}$ 表示对最后两个维度的转置。

  对于每个查询块 $i \in [0, N_q - 1]$， 我们选择得分最高的前 $r$ 个键块。

  据此可以构建一个二值掩码矩阵 $M \in \mathbb{R}^{b \times n_h \times s_q \times s_k}$，定义如下：

  $M[:, :, i n : (i + 1)n, j n : (j + 1)n] = \begin{cases} 1, & \text{若键块 } j \text{ 属于查询块 } i \text{ 的 top-}r \text{ 邻居;} \\ 0, & \text{否则.} \end{cases}$

• 带块选择掩码的注意力计算（Attention with Block Selection Mask）

  最后，我们计算加掩码的注意力。

  注意力得分矩阵 $S$ 定义为：

  $S = \frac{Q K^{\top}}{\sqrt{d}} \in \mathbb{R}^{b \times n_h \times s_q \times s_k},$

  其中 $K^{\top}$ 表示对最后两个维度的转置。

  然后我们应用掩码：

  $S_{\text{masked}} = \begin{cases} S, & \text{当 } M = 1, \\ -\infty, & \text{当 } M = 0. \end{cases}$

  最终的注意力权重通过对最后一个维度应用 softmax 得到：$O = \text{softmax}(S_{\text{masked}}).$

（2）环形块稀疏注意力（Ring Block Sparse Attention）在上下文并行中的建模 Link to （2）环形块稀疏注意力（Ring Block Sparse Attention）在上下文并行中的建模

我们将稀疏注意力计算扩展到上下文并行（context parallelism）。

给定一个张量并行的规模 $N_{cp}$，每个并行 rank 维护输入张量 $\frac{T \times H \times W}{N_{cp}}$ 的局部片段。

设 $Q_i, K_i, V_i \in \mathbb{R}^{b \times n_h \times \frac{T \times H \times W}{N_{cp}} \times d}$

分别表示第 $i$ 个 rank 的查询（query）、键（key）和值（value）张量。

• 局部块选择掩码的构建（Local Block Selection Mask Construction）

  为了计算第 $i$ 个 rank 的块稀疏注意力掩码 $M_i \in \mathbb{R}^{b \times n_h \times \frac{N_q}{N_{cp}} \times N_k}$，

  每个 rank 首先计算其自身的局部池化键（local pooled keys）：

  $K_{\text{pool}, j}[:, :, b_j, :] = \frac{1}{n} \sum_{m=0}^{n-1} K_j[:, :, (b_j - 1)n + m, :] \quad \text{其中 } b_j = 1, \ldots, \frac{s_k}{N_{cp}},$

  其中 $K_j = K[:, :, (j-1)\frac{s_k}{N_{cp}} : j\frac{s_k}{N_{cp}}, :], \quad j \in [1, N_{cp}].$

  然后我们收集所有池化键的表示，并计算 rank $i$ 的池化得分矩阵：$S_{\text{pool}, i} = \frac{ Q_{\text{pool}, i} \left( \bigoplus_{j=1}^{N_{cp}} K_{\text{pool}, j} \right)^{\top} }{\sqrt{d}},$

  其中符号 $\bigoplus$ 表示沿序列维度的拼接， 并且 $Q_i = Q[:, :, (i-1)\frac{s_q}{N_{cp}} : i\frac{s_q}{N_{cp}}, :], \quad i \in [1, N_{cp}].$

  根据 $S_{\text{pool}, i}$，掩码 $M_i$ 通过为每个批次和注意力头选择前 $r$ 个最高分的键块（key block）构建而成。

  为了优化效率，我们采用一种环形注意力（ring-attention）通信模式， 使得局部池化得分的计算与相邻 rank 间的 $K_{\text{pool}, i}$ 张量通信相互重叠

• 带有局部块选择掩码的环形注意力（Ring Attention with Local Block Selection Mask）

  一旦获得 $M_i$，每个 rank 就会根据 $M_{ij} \in \mathbb{R}^{b \times n_h \times \frac{N_q}{N_{cp}} \times \frac{N_k}{N_{cp}}}$ 计算其注意力输出 $O_i$，其中 $M_{ij}$ 是与 rank $j$ 对应的掩码块。

  在线 softmax 算法用于该过程。 此外，环形注意力算法（Ring-attention，Liu et al., 2023）被改进以使注意力计算与 $K_j, V_j$ 的通信重叠执行。

简单总结 Link to 简单总结

• 背景问题

  在普通的自注意力（Self-Attention）中，每个 token 都要和所有其他 token 计算注意力分数：$S = \frac{QK^\top}{\sqrt{d}}$

  如果输入序列很长（比如视频帧、图像块），这个计算非常大，复杂度是 $O(n^2)$。

• 核心思想：“分块 + 稀疏”

  把输入（例如视频的时间-高度-宽度维度）分成多个 3D 小块：

  • 每个块内部的信息相似；
  • 块之间的联系比块内部稀疏；
  • 所以我们只在部分块之间计算注意力，而不是全部。

  这样注意力矩阵 $S$ 就从“密集”变成了“稀疏”，即 Block Sparse Attention（块稀疏注意力）。

• 怎么选哪些块要计算？——“块选择掩码 Mask”

  每个块会先做平均池化（pooling），得到一个代表性的“块向量”；

  计算所有块之间的相似度（得分矩阵 $S_{pool}$）；

  为每个查询块挑出得分最高的前 $r$ 个键块；

  构建一个二值掩码 $M$：

  • $M=1$ → 这两个块要计算注意力；
  • $M=0$ → 不计算。

  最后用 $M$ 掩码掉不需要计算的部分，只对重要块做 softmax。

  这样，计算量大大降低，但还能保持模型对重要关系的捕捉。