Self Forcing: Bridging the Train-Test Gap in Autoregressive Video Diffusion Link to Self Forcing: Bridging the Train-Test Gap in Autoregressive Video Diffusion

https://arxiv.org/pdf/2506.08009

DiT通过双向注意力同时对所有帧进行去噪，允许未来影响过去，并要求一次性生成整个视频，限制了其在实时流式应用中的适用性，因为在生成当前帧时未来信息是未知的。

AR模型按照顺序生成视频，这种范式自然与时间媒体的因果结构一致。然而，由于依赖有损向量量化技术，AR 模型通常难以匹敌最新视频扩散模型所达到的视觉保真度。

使视频扩散模型具备 AR 生成能力：Teacher Forcing（TF） 和 Diffusion Forcing（DF）。

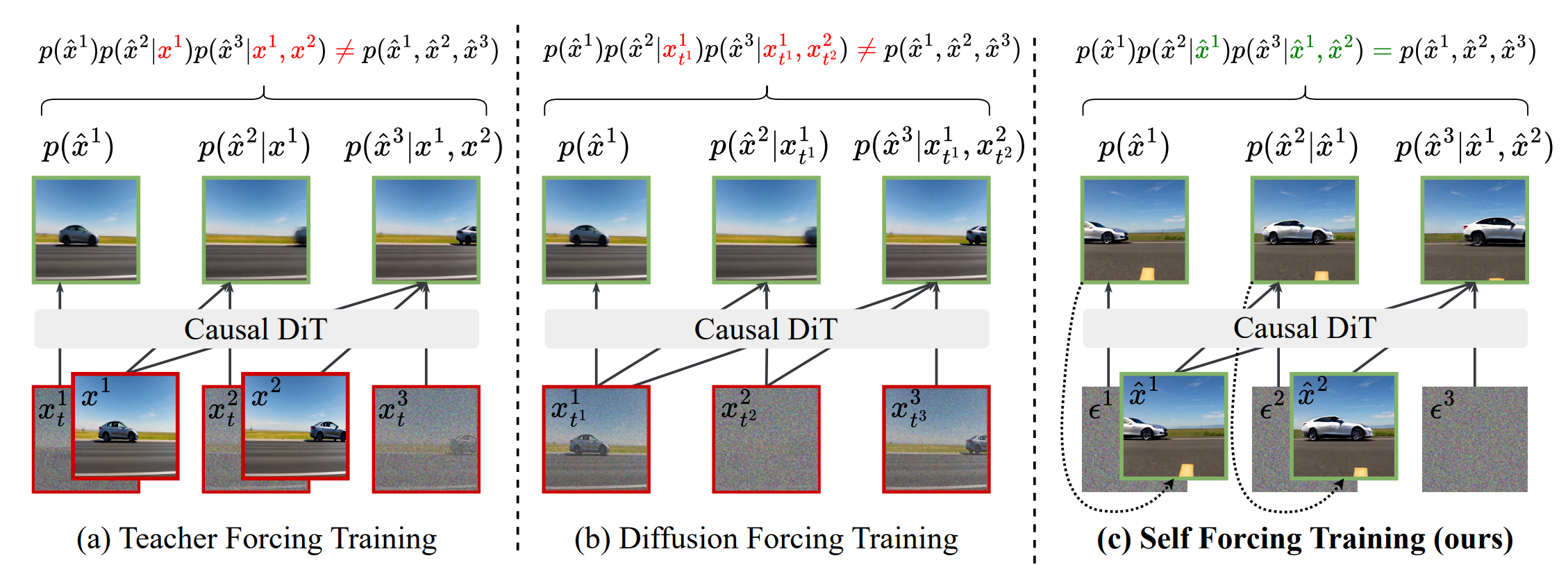
TF 使用真实、干净的上下文帧对每一帧进行去噪（如图 $1(a)$），通常被称为下一帧预测。

DF 在具有不同噪声等级的视频上训练模型：每一帧的噪声独立采样，然后模型基于带噪声的上下文，对当前帧去噪（如图 $1(b)$）。

缺点：

• 曝光偏差（exposure bias）：

  使用 TF 或 DF 训练的模型在自回归生成过程中常出现误差累积，导致视频质量随时间下降。

  模型仅在真实上下文上训练，但在推理时必须依赖自身不完美的预测，随着生成过程推进，这会导致分布不匹配，并不断放大误差。

  尽管一些方法尝试在推理阶段引入噪声上下文以缓解此问题，但这种设计牺牲时间一致性、复杂化 KV 缓存、增加生成延迟，并不能从根本上解决曝光偏差。

受到早期 RNN 序列模型技术的启发，**Self Forcing（SF）**方法通过在训练阶段显式展开自回归生成过程来弥合训练—测试分布差距，使每一帧基于模型先前自生成的帧，而非真实帧进行生成。

这允许在完整生成的视频序列上施加整体式的分布匹配损失。通过迫使模型在训练中接触并从自身预测误差中学习，Self Forcing 有效减轻曝光偏差并减少误差累积。

我们的工作与 CausVid最为接近，它训练少步自回归扩散模型，使用 DF 方案与分布匹配蒸馏（DMD）。然而，CausVid 受到一个关键问题的影响：其训练输出（由 DF 生成）来自错误的分布，因此 DMD 损失匹配的是错误的目标分布。我们的方法通过直接在模型自身预测上进行训练并从根源上解决此问题，使模型输出与真实目标分布对齐。

3 Self Forcing：通过整体式后训练弥合训练–测试分布差距 Link to 3 Self Forcing：通过整体式后训练弥合训练–测试分布差距

3.1 预备知识：自回归视频扩散模型（Autoregressive Video Diffusion Models） Link to 3.1 预备知识：自回归视频扩散模型（Autoregressive Video Diffusion Models）

自回归视频扩散模型是一类混合生成模型，它将自回归链式法则分解与用于视频生成的去噪扩散模型结合起来。给定一个由 $N$ 个视频帧组成的序列 $x^{1:N} = (x^1, x^2, \ldots, x^N)$，联合分布可通过链式法则分解为 $p(x^{1:N}) = \prod_{i=1}^N p(x^i \mid x^{<i})$。

其中，每个条件分布 $p(x^i \mid x^{<i})$ 使用扩散过程建模：逐步去噪一个最初的高斯噪声样本，条件依赖于先前生成的帧。该方法结合了自回归模型的时序依赖与扩散模型对连续视觉信号高质量建模的能力。

在实践中，我们也可以选择一次生成一组帧（chunk），而不是单一帧。为了方便，本节仍以单帧作为基本单位。

大多数自回归视频扩散模型使用 Teacher Forcing（TF）或 Diffusion Forcing（DF）范式，通过逐帧去噪损失进行训练。具体而言，每个噪声帧 $x_t^i$ 来自前向过程 $q_t(x_t^i \mid x_0^i)$，

并满足： $x_t^i = \Psi(x_0^i, \epsilon^i, t^i) = \alpha_{t^i} x_0^i + \sigma_{t^i} \epsilon^i$，

其中 $\alpha_t, \sigma_t$ 是在有限时间区间 $t^i \in [0,1000]$ 上预定义的噪声调度，$\epsilon^i \sim \mathcal{N}(0, I)$ 为高斯噪声。

TF 将时间步 $t^i$ 在所有帧间共享，而 DF 则为每帧独立采样 $t^i$。生成模型通过时间反演过程学习，每个去噪步骤通过预测噪声 $\hat{\epsilon}_\theta^i := G_\theta(x_t^i, t^i, c)$ 实现，其中 $c$ 为上下文。上下文由 TF 中的干净真实帧 $x^{<i}$ 或 DF 中的噪声上下文帧 $x_t^{j<i}$ 组成。模型通过最小化帧级均方误差（MSE）进行训练：

$\mathcal{L}_{\mathrm{DM}}^i = \mathbb{E}_{x_0^i, x_t^i, \epsilon^i} \left[w_{t^i} \| \hat{\epsilon}_\theta^i - \epsilon^i \|^2 \right],$其中 $w_t$ 是权重函数。

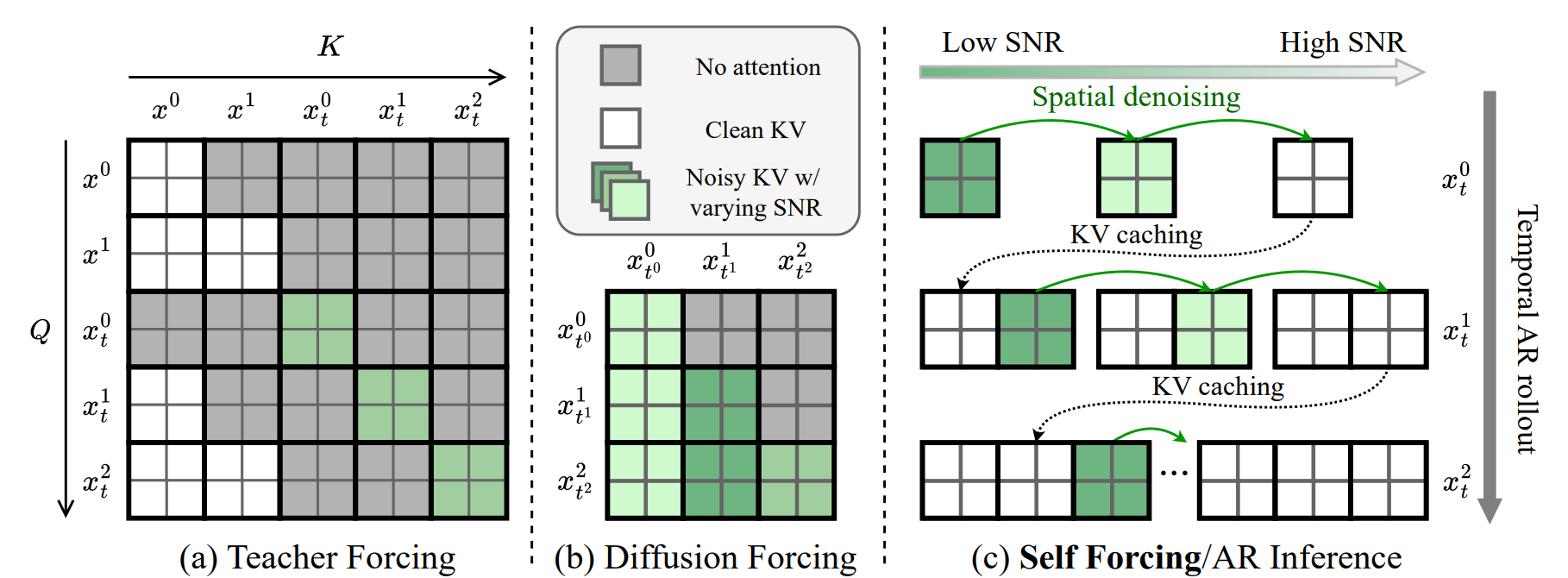
我们关注带文本条件的视频扩散模型，其基于 Transformer [62] 并运行在由因果 3D VAE [37] 编码的压缩潜空间上。自回归链式法则通过因果注意力实现。图 2(a) 和 2(b) 展示了 Teacher Forcing 与 Diffusion Forcing 的注意力 mask 配置。

在 TF 中，我们介绍一种效率更高的变体：使用稀疏注意力 mask 并行处理所有帧，而不是在每次训练中逐帧去噪 [33]。这种设计也被用于 MAR-based 自回归视频生成 [43] 和其他自回归视频扩散模型 [106, 107]。

3.2 通过自我展开进行自回归扩散后训练（Autoregressive Diffusion Post-Training via Self-Rollout） Link to 3.2 通过自我展开进行自回归扩散后训练（Autoregressive Diffusion Post-Training via Self-Rollout）

Self Forcing 的核心思想，是在训练过程中通过自回归自我展开（self-rollout）生成视频，从而遵循推理阶段的生成流程。

具体而言，采样一批视频 $\{x_\theta^{1:N}\} \sim p_\theta(x^{1:N}) = \prod_{i=1}^N p_\theta(x^i \mid x^{<i})$，

其中每一帧 $x^i$ 都是通过迭代去噪生成的，条件依赖于模型先前自生成的输出，包括过去的干净上下文帧，以及当前时间步的噪声上下文帧。

不同于以往仅在推理阶段使用 KV 缓存的自回归模型，我们的 Self Forcing 方法在训练过程中创新性地引入了 KV 缓存，如图 2(c) 所示。

然而，若使用标准的多步扩散模型实现 Self Forcing，会因需展开并反向传播整个长去噪链而导致计算成本过高。因此，我们选用少步扩散模型 $G_\theta$ 来近似自回归分解中的每个条件分布 $p_\theta(x^i \mid x^{<i})$。

考虑时间步子序列 $\{t_0 = 0,\; t_1,\; \ldots,\; t_T = 1000\}$，它是区间 $[0,\ldots,1000]$ 的一个子序列。

在每一个去噪时间步 $t_j$ 和帧索引 $i$ 下，模型对中间噪声帧 $x_{t_j}^i$ 进行去噪，条件依赖于之前的干净帧 $x^{<i}$。随后，模型通过前向过程 $\Psi$ 向该去噪帧中注入低噪声级别的高斯噪声，从而生成下一时间步的噪声帧 $x_{t_{j-1}}^i$ 作为下一步去噪的输入。这与少步扩散模型中的标准做法一致。

模型分布 $p_\theta(x^i \mid x^{<i})$ 隐式定义为若干函数复合： $f_{\theta,t_1} \circ f_{\theta,t_2} \circ \ldots \circ f_{\theta,t_T}(x_{t_T}^i)$，

其中 $f_{\theta,t_j}(x_{t_j}^i) = \Psi\!\left(G_\theta(x_{t_j}^i,\; t_j,\; x^{<i}),\; \epsilon_{t_{j-1}},\; t_{j-1}\right)$， 并且 $x_{t_T}^i \sim \mathcal{N}(0, I)$。

即使采用少步扩散模型，若朴素地对整个自回归扩散过程执行反向传播，仍会导致显存消耗过大。为此，我们提出梯度截断策略，将反向传播限制到每一帧的最后一个去噪步骤。

此外，与推理时始终执行 $T$ 步去噪不同，我们在每次训练迭代中，从区间 $[1, T]$ 中随机采样一个去噪步骤 $s$，并将第 $s$ 步的去噪结果作为最终输出。该随机采样策略确保所有中间去噪步骤都能获得监督信号。

我们还限制梯度从当前帧流向 KV 缓存嵌入，从而切断梯度向前传播，避免过去帧在训练中收到来自当前帧的梯度。完整的训练流程详见算法 1。

Require: 去噪时间步集合 $\{t_1, \ldots, t_T\}$
Require: 视频帧数 $N$
Require: 自回归扩散模型 $G_\theta$（通过 $G_\theta^{\mathrm{KV}}$ 返回 KV 嵌入）

1: loop
2:     初始化模型输出 $X_\theta \leftarrow []$
3:     初始化 KV 缓存 $\mathrm{KV} \leftarrow []$
4:     采样 $s \sim \mathrm{Uniform}(1, 2, \ldots, T)$
5:     for $i = 1, \ldots, N$ do
6:         初始化噪声帧 $x_{t_T}^i \sim \mathcal{N}(0, I)$
7:         for $j = T, \ldots, s$ do
8:             if $j = s$ then
9:                 启用梯度计算
10:                 设 $\hat{x}_0^i \leftarrow G_\theta(x_{t_j}^i, t_j, \mathrm{KV})$
11:                 $X_\theta.\mathrm{append}(\hat{x}_0^i)$
12:                 禁用梯度计算
13:                 缓存 KV：$\mathrm{kv}^i \leftarrow G_\theta^{\mathrm{KV}}(\hat{x}_0^i; 0, \mathrm{KV})$
14:                 $\mathrm{KV}.\mathrm{append}(\mathrm{kv}^i)$
15:             else
16:                 禁用梯度计算
17:                 设 $\hat{x}_0^i \leftarrow G_\theta(x_{t_j}^i, t_j, \mathrm{KV})$
18:                 采样 $\epsilon \sim \mathcal{N}(0, I)$
19:                 设
    $x_{t_{j-1}}^i \leftarrow \Psi(\hat{x}_0^i, \epsilon, t_{j-1})$
20:             end if
21:         end for
22:     end for
23:     根据分布匹配损失更新参数 $\theta$
24: end loop

3.3 整体式分布匹配损失（Holistic Distribution Matching Loss） Link to 3.3 整体式分布匹配损失（Holistic Distribution Matching Loss）

自回归自我展开直接从推理时的模型分布中生成样本，使我们能够对生成的视频分布 $p_\theta(x^{1:N})$ 应用整体式视频级损失，使其与真实视频分布 $p_{\mathrm{data}}(x^{1:N})$ 对齐。

为利用预训练扩散模型并增强稳定性，我们向两个分布注入噪声，匹配 $p_{\theta,t}(x_t^{1:N})$ 与 $p_{\mathrm{data},t}(x_t^{1:N})$，

其中每个代表扩散前向过程后的对应分布：$p_{\cdot,t}(x_t^{1:N}) = \int q_{t\mid 0}(x_t^{1:N} \mid x^{1:N}) p_\cdot(x^{1:N}) dx^{1:N}$。

我们的框架适用于多种散度度量与分布匹配方法，本文中我们考虑三类：

• Distribution Matching Distillation（DMD） Link to • Distribution Matching Distillation（DMD）

该方法最小化反向 KL 散度 $\mathbb{E}_t[D_{\mathrm{KL}}(p_{\theta,t} \,\|\, p_{\mathrm{data},t})]$， 通过分数差异引导分布对齐。

• Score Identity Distillation（SiD） Link to • Score Identity Distillation（SiD）

该方法使用 Fisher 散度 $\mathbb{E}_{t,p_\theta}\left[\| \nabla \log p_{\theta,t} - \nabla \log p_{\mathrm{data},t} \|^2 \right]$ 进行分布匹配。

• 生成对抗网络（GANs） Link to • 生成对抗网络（GANs）

通过最小化 Jensen–Shannon 散度训练一个判别器，用以区分生成样本与真实样本。

关键的是，我们的训练目标匹配整体式视频序列分布 $D(p_{\mathrm{data}}(x^{1:N}) \| p_\theta(x^{1:N}))$。

相比之下，TF/DF 的帧级分布匹配可写为：$\mathbb{E}_{x^{<i} \sim p_{\mathrm{data}}} D_{\mathrm{KL}}(p_{\mathrm{data}}(x^i \mid x^{<i}) \| p_\theta(x^i \mid x^{<i}))$，

其中 DF 从噪声扰动的数据中采样上下文帧。此类范式会改变训练动态，使上下文帧来自模型自身分布而非真实分布，从而导致曝光偏差。我们的整体式损失强迫模型从自身误差中学习，提升鲁棒性。

尽管这些目标曾用于扩散模型的时间步蒸馏，但我们的目标并非加速采样，而是提高自回归视频生成质量。与 CausVid 不同，我们的模型训练分布与推理分布一致，因此不会出现分布偏移问题。

3.4 使用滚动 KV Cache 的长视频生成 Link to 3.4 使用滚动 KV Cache 的长视频生成

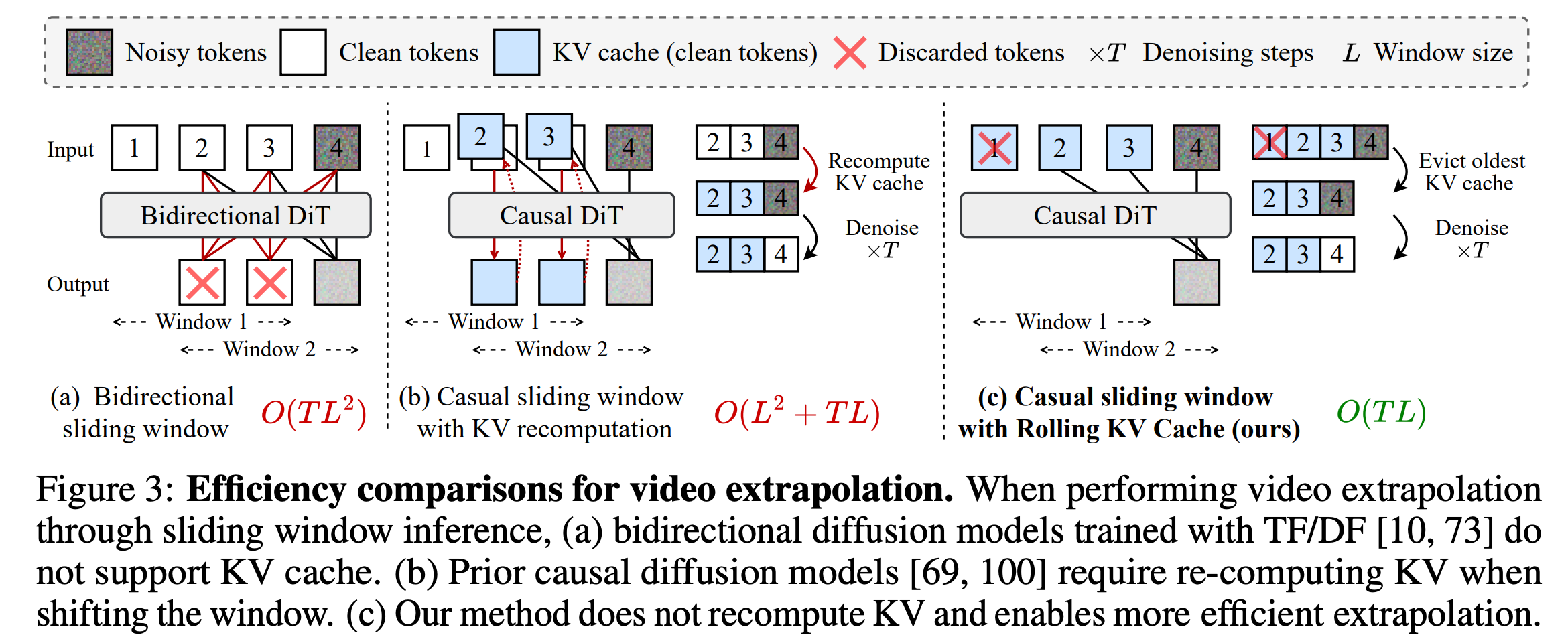
自回归模型相较标准视频扩散模型的主要优势之一在于其可外推性，使得理论上可以通过滑动窗口推理无限生成长视频。

使用 Diffusion Forcing 的双向注意力模型也可以自回归生成视频，但它们不支持 KV Cache，因此每个新帧都需要完全重新计算注意力矩阵，复杂度为 $O(T L^2)$（$T$ 为去噪步数，$L$ 为窗口大小），如图 3(a)。

具有因果注意力的模型可借助 KV Cache 提升效率。

然而，现有方法需要对重叠窗口重复构建 KV Cache，如图 3(b)，其复杂度为 $O(L^2 + T L)$。

因此实际实现通常采用较大步幅滑动窗口，牺牲时间一致性。

受大语言模型的研究启发，我们提出一种滚动 KV Cache，使自回归扩散模型无需重建 KV Cache 即可生成无限长视频。

如图 3(c)，我们维护一个固定大小的 KV Cache，存储最近 $L$ 帧的 KV；每次生成新帧时检查缓存是否已满，若是则移除最旧项并加入新项。该方法具有 $O(T L)$ 的时间复杂度，并在每次生成新帧时保持一致的上下文长度。

算法 2 给出了滚动 KV Cache 下的自回归长视频生成流程。

然而，直接实现会导致分布不匹配：第一帧具有不同统计性质，因为它未进行时间压缩。模型因此无法泛化，图像潜变量在滚动 KV 中丢失。我们的解决方案是限制窗口，使模型在训练中永远不在第一帧上去噪最后一步。这样模型在长视频生成时即可处理最终 chunk 所遇到的条件分布。