From Slow Bidirectional to Fast Autoregressive Video Diffusion Models Link to From Slow Bidirectional to Fast Autoregressive Video Diffusion Models

https://arxiv.org/pdf/2412.07772

https://github.com/tianweiy/CausVid

问题：

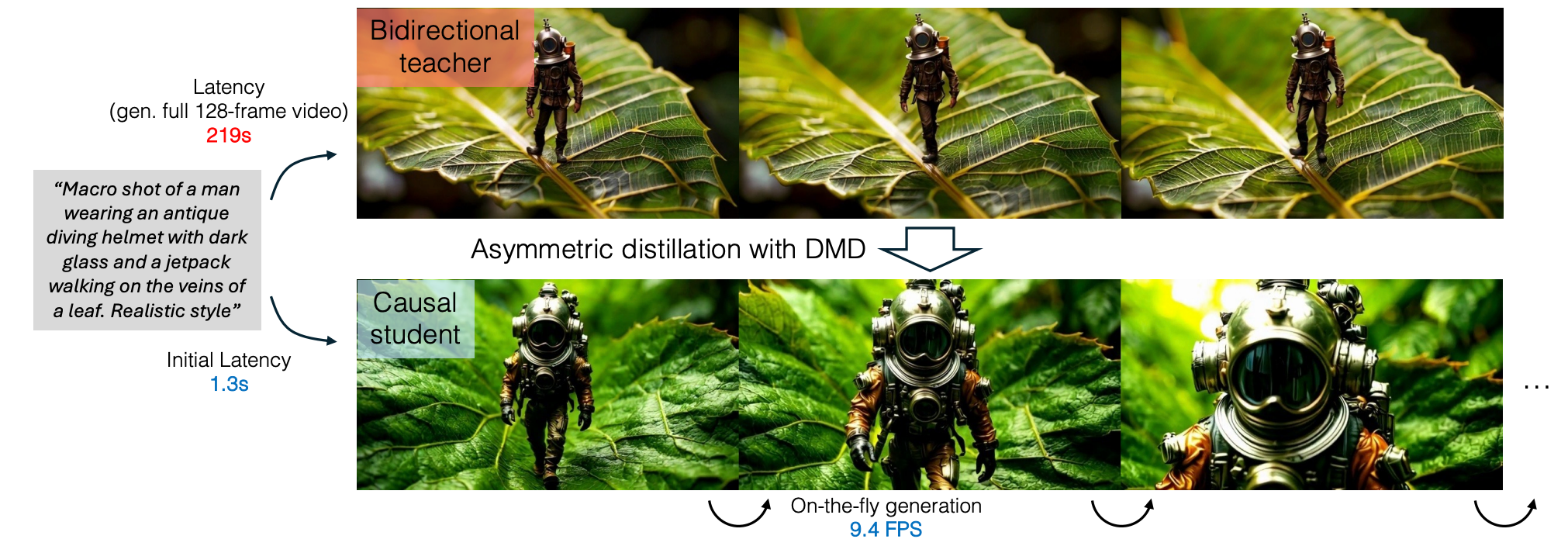
• 当前的视频扩散模型==双向注意力依赖==，在交互式应用中面临困难
• 生成单帧就需要==模型处理整个序列==，包括未来帧

方法：

• 将一个预训练的双向扩散 Transformer ==适配为自回归 Transformer==，使其能够即时生成帧

• 将==分布匹配蒸馏（DMD）==扩展到视频领域，将一个 50 步的扩散模型蒸馏为 4 步生成器，进一步降低降低延迟

  为实现稳定且高质量的蒸馏，提出了

  • ==一种基于教师 ODE 轨迹的学生初始化方案==
  • ==一种由双向教师监督因果学生模型的非对称蒸馏策略==

  有效减轻了自回归生成中的==误差累积==，使模型即便只在短片段上训练，也能实现长时段的视频合成

分布匹配蒸馏（Distribution Matching Distillation, DMD） Link to 分布匹配蒸馏（Distribution Matching Distillation, DMD）

分布匹配蒸馏（DMD）是一种将缓慢的、多步教师扩散模型蒸馏为高效少步学生模型的技术。

其核心思想是在随机时间步 $t$ 上，最小化平滑后的数据分布 $p_{\text{data}}(x_t)$ 与学生生成器分布$p_{\text{gen}}(x_t)$ 之间的反向 KL 散度。

其反向 KL 的梯度可由两个得分函数的差值近似表示为：

其中：

• $\Psi$：前向扩散过程
• $\epsilon \sim \mathcal{N}(0, I)$：高斯噪声
• $G_\phi$：由参数 $\phi$ 控制的生成器
• $s_{\text{data}}$、$s_{\text{gen}}$：分别为基于数据与生成器分布训练得到的得分函数$s_{\theta}(\mathbf{x}_t, t) = \nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t) = - \frac{\mathbf{\epsilon}_{\theta}(\mathbf{x}_t, t)}{\sigma_t}$

在训练中，DMD从一个预训练的扩散模型初始化两个得分函数

• data的得分函数保持冻结；
• gen的得分函数通过生成器的输出在线训练；
• 同时，生成器通过公式（1）获得梯度，使其输出逐渐匹配数据分布。

DMD2 将 DMD 从单步扩展到多步生成，方法为：不再使用纯噪声输入 $\epsilon$，而改为使用部分去噪的中间图像 $x_t$，从而进一步提升训练稳定性与生成质量。

Methods Link to Methods

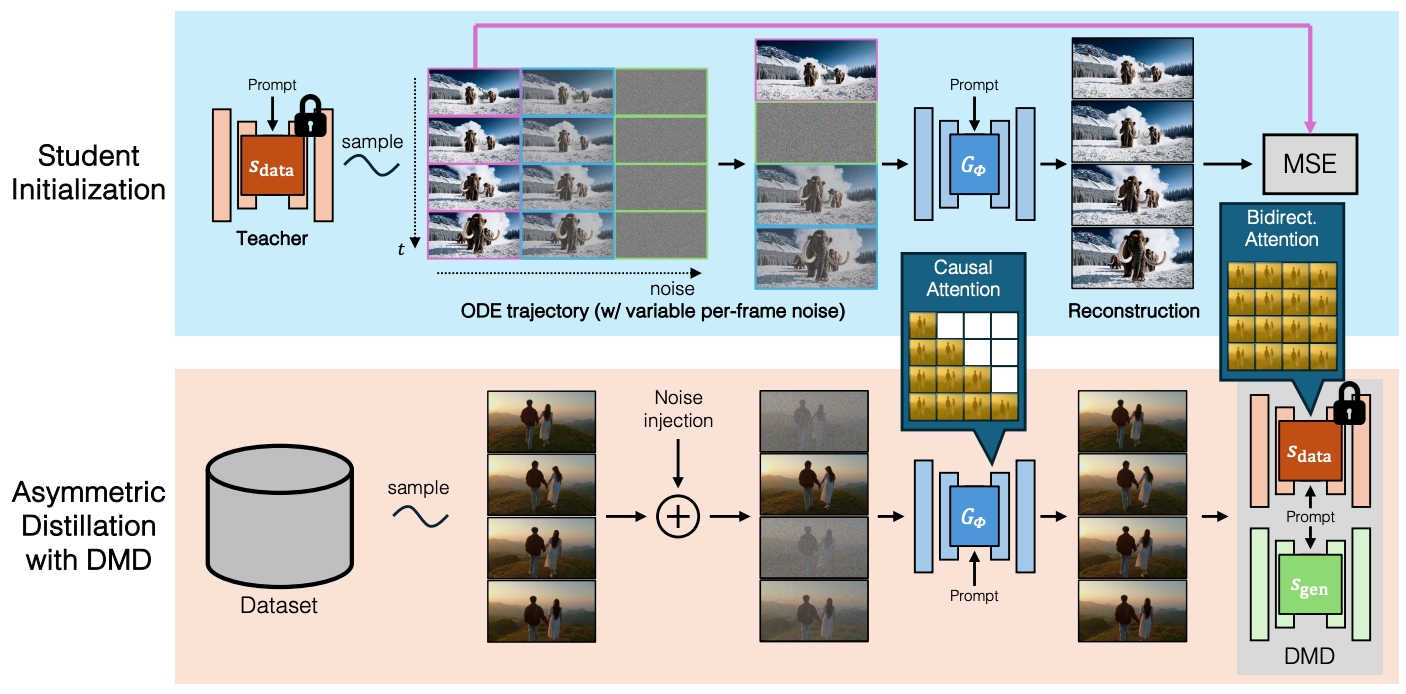
Overview

4.1 自回归架构（Autoregressive Architecture） Link to 4.1 自回归架构（Autoregressive Architecture）

首先 3D VAE 压缩视频。

VAE 编码器独立处理每个视频帧块，将其压缩为更短的潜帧块，解码器随后从每个潜帧块重建原始视频帧。

因果DiT在这一潜空间中工作，按顺序生成潜在帧。

设计了一种 块级因果注意力机制，灵感来自结合自回归模型与扩散模型的先前研究。

在每个块内部，我们应用 双向自注意力 来捕获局部时间依赖、保持一致性。

为了实现因果性，我们在不同块之间应用因果注意力，使当前块的帧不能访问未来块的帧。

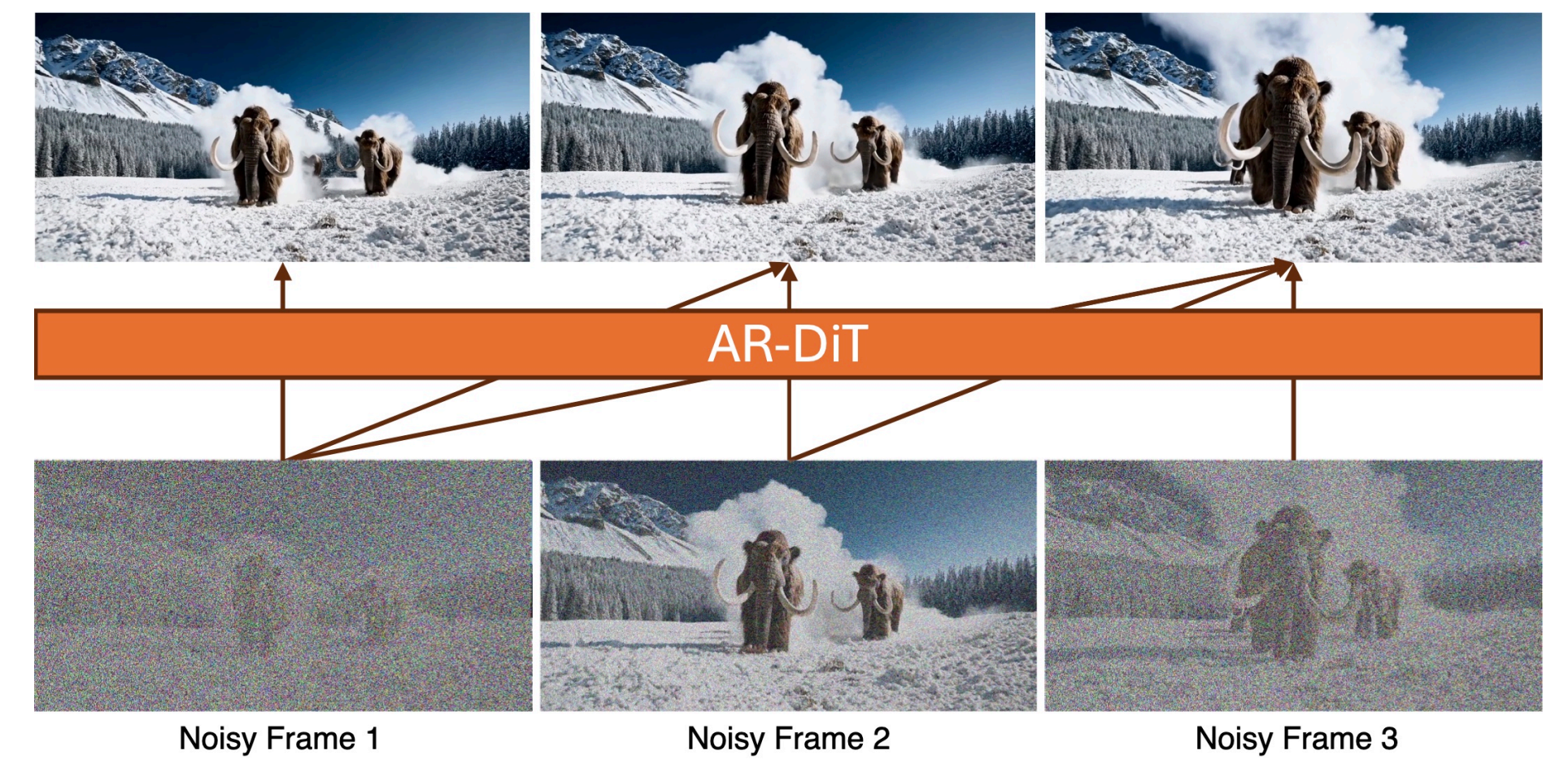
Tokens in the current frame only attend to tokens from current and previous frames, but not the future.

我们的设计与完全因果注意力具有相同的延迟，因为 VAE 解码器生成像素仍然至少需要一个潜帧块。

形式化地，我们定义注意力 mask $M$ 为：

其中 $i$ 和 $j$ 表示序列中的帧索引，$k$ 为块大小，$\lfloor \cdot \rfloor$ 表示向下取整。

我们的扩散模型 $G_\phi$ 基于 DiT 架构，扩展用于自回归视频生成。

我们将 块级因果注意力 mask 添加到自注意力层中（如图所示），同时保持核心结构不变，从而可利用预训练的双向模型权重，以实现更快的收敛。

4.2 双向 → 因果生成器蒸馏（Bidirectional → Causal Generator Distillation） Link to 4.2 双向 → 因果生成器蒸馏（Bidirectional → Causal Generator Distillation）

一种直接的方法是通过蒸馏因果教师模型来训练少步因果生成器。

这包括将预训练的双向 DiT 模型适配为上述因果注意力机制并使用去噪损失$\mathcal{L}(\theta) = \mathbb{E}_{t,\mathbf{x}_0,\mathbf{\epsilon}} \| \mathbf{\epsilon}_{\theta}(\mathbf{x}_t, t) - \mathbf{\epsilon} \|_2^2$微调。

训练时，模型输入 $N$ 个噪声视频帧，这些帧被分为 $L$ 个块：

• $\{ x_t^i \}_{i=1}^L$，其中 $i \in \{1,2,\ldots,L\}$ 为块索引
• 每个块 $x_t^i$ 拥有独立的噪声时间步 $t^i \sim [0,999]$，遵循 Diffusion Forcing

推理时，模型按顺序对每个块进行去噪，条件为已生成的前序干净块。

尽管蒸馏这一微调后的自回归扩散教师模型理论上可行，但初步实验表明结果不佳。

由于因果扩散模型弱于双向扩散模型，从较弱教师蒸馏会限制学生性能。

此外，误差累积也会从教师传播到学生。

为克服因果教师的局限性，我们提出非对称蒸馏（asymmetric distillation）：

• 教师模型使用双向注意力
• 学生模型被限制为因果注意力

训练流程：

前提：

• 少步去噪时间步集合 $\mathcal{T} = \{0, t_1, t_2, \ldots, t_Q\}$
• 视频长度 $N$
• 块大小 $k$
• 预训练的双向教师模型 $s_{\text{data}}$
• 数据集 $\mathcal{D}$

1. 使用 ODE 回归初始化学生模型 $G_\phi$（见 Sec. 4.3）
2. 将生成器输出的得分函数 $s_{\text{gen},\xi}$ 初始化为 $s_{\text{data}}$
3. while train do
4. ​ 从数据集中采样一个视频，并将视频帧划分为$L = \lceil N / k \rceil$ 个块，$\{ x_0^i \}_{i=1}^{L} \sim \mathcal{D}$
5. ​ 为每个块采样时间步：$\{ t^i \}_{i=1}^{L} \sim \text{Uniform}(\mathcal{T})$
6. ​ 添加噪声：$x_{t^i}^i = \alpha_{t^i} x_0^i + \sigma_{t^i} \epsilon^i,\quad \epsilon^i \sim \mathcal{N}(0, I)$
7. ​ 使用学生模型（带块级因果 mask）预测干净帧：$\hat{x}_0 = G_\phi\big(\{ x_{t^i}^i \}, \{ t^i \} \big)$
8. ​ 采样单个时间步：$t \sim \text{Uniform}(0, T)$
9. ​ 向预测添加噪声：$\hat{x}_t = \alpha_t \hat{x}_0 + \sigma_t \epsilon,\quad \epsilon \sim \mathcal{N}(0, I)$
10. ​ 使用 DMD 损失 更新学生模型 $G_\phi$（在前面DMD写了）
11. ​ 训练生成器的得分函数 $s_{\text{gen},\xi}$：
12. ​ 采样新噪声 $\epsilon' \sim \mathcal{N}(0, I)$
13. ​ 生成新的噪声样本：\hat{x}_t^{\,'} = \alpha_t \hat{x}_0 + \sigma_t \epsilon'
14. ​ 计算去噪损失，并更新 $s_{\text{gen},\xi}$ $\mathcal{L}(\theta) = \mathbb{E}_{t,\mathbf{x}_0,\mathbf{\epsilon}} \| \mathbf{\epsilon}_{\theta}(\mathbf{x}_t, t) - \mathbf{\epsilon} \|_2^2.$
15. end while

4.3 学生模型初始化（Student Initialization） Link to 4.3 学生模型初始化（Student Initialization）

由于架构差异，直接使用 DMD 损失训练因果学生模型会不稳定。

为解决此问题，引入一种高效的初始化策略。

生成一个由双向教师模型产生的 ODE 解对组成的小型数据集：

• 从高斯分布 $\mathcal{L}(0, I)$ 中采样噪声输入 $\{ x_T^i \}_{i=1}^L$
• 使用 ODE 求解器，通过教师模型模拟逆扩散，得到对应的 ODE 轨迹$\{ x_t^i \}_{i=1}^L$，其中 $t$ 从 $T$ 到 0 覆盖全部推理时间步

从 ODE 轨迹中，我们选择与学生生成器所用时间步一致的一部分 $t$ 值。

学生模型随后使用以下回归损失在此数据集上训练：

其中少步生成器 $G_\phi$ 从教师模型初始化。

该 ODE 初始化计算量低，仅需少量训练迭代和少量的 ODE 解对即可稳定训练。

4.4 基于 KV 缓存的高效推理（Efficient Inference with KV Caching） Link to 4.4 基于 KV 缓存的高效推理（Efficient Inference with KV Caching）

推理阶段，我们使用带 KV 缓存的自回归扩散 Transformer 顺序生成视频帧，从而实现高效推理。

详细的推理流程见 Algorithm 2：

前提：

• 去噪时间步集合 $\{ t_0 = 0, t_1, \ldots, t_Q \}$
• 视频长度 $N$
• 块大小 $k$
• 少步自回归视频生成器 $G_\phi$

1. 将视频帧划分为 $L = \lceil N / k \rceil$ 个块
2. 初始化 KV 缓存：$\mathcal{C} \leftarrow \varnothing$
3. for $i = 1$ to $L$ do
4. ​ 初始化当前块：$x_{t_Q}^i \sim \mathcal{N}(0, I)$
5. ​ 在时间步上迭代去噪：
6. ​ for $j = Q$ to $1$ do
7. ​ 生成输出（使用缓存）：$\hat{x}_{t_j}^i = G_\phi(x_{t_j}^i, t_j)$
8. ​ 更新块：$x_{t_{j-1}}^i = \alpha_{t_j} \hat{x}_{t_j}^i + \sigma_{t_j} \epsilon', \quad \epsilon' \sim \mathcal{N}(0, I)$
9. ​ end for
10. ​ 更新 KV 缓存：
11. ​ 通过一次前向传播计算 KV 对：$G_\phi(x_0^i, 0)$
12. ​ 将新的 KV 对追加至缓存 $\mathcal{C}$
13. end for
14. 返回生成的帧序列 $\{ x_0^i \}_{i=1}^L$

值得注意的是，由于使用了 KV 缓存，推理阶段不再需要块级因果注意力。

这使我们能够利用快速双向注意力实现Flash Attention，进一步提升推理速度。

讨论（Discussion） Link to

尽管我们的方法能够生成高质量视频（最长 30 秒），但在生成极长视频时仍会出现质量下降。

开发更有效的策略来应对误差累积仍是未来工作方向。

此外，虽然我们的延迟显著降低——比之前的方法低多个数量级——它仍然==受限于当前的 VAE 设计==，该设计要求在生成任何像素之前生成五个潜帧。采用更高效的逐帧 VAE 能将延迟再降低一个数量级，从而显著提升模型响应速度。

最后，虽然我们的方法在使用 DMD 目标时能生成高质量样本，但其输出多样性有所降低，这也是基于反向 KL 分布匹配方法的典型限制。

未来工作可探索替代目标，如 EM-Distillation和 Score Implicit Matching，以更好地保持输出多样性。

目前，我们的实现生成视频的帧率约为 10 FPS，但通过标准工程优化（包括模型编译、量化和并行化）有望实现实时性能。