Diffusion Forcing: Next-token Prediction Meets Full-Sequence Diffusion Link to Diffusion Forcing: Next-token Prediction Meets Full-Sequence Diffusion

https://arxiv.org/pdf/2407.01392

https://github.com/buoyancy99/diffusion-forcing

https://zhuanlan.zhihu.com/p/9658499592

当前的next token prediction模型通常通过 teacher forcing进行训练，其中模型基于真实的历史 token 来预测紧接着的下一个 token。

这样会带来两个限制：

• 没有一种机制可以引导序列采样以最小化某个特定目标；

• 当前的下一 token 模型在处理连续数据时容易变得不稳定。

  例如，在尝试自回归地生成视频（相比生成文本或向量量化的潜变量）时，只要超过训练时长，逐帧预测中的轻微错误就会累积，从而导致模型发散。

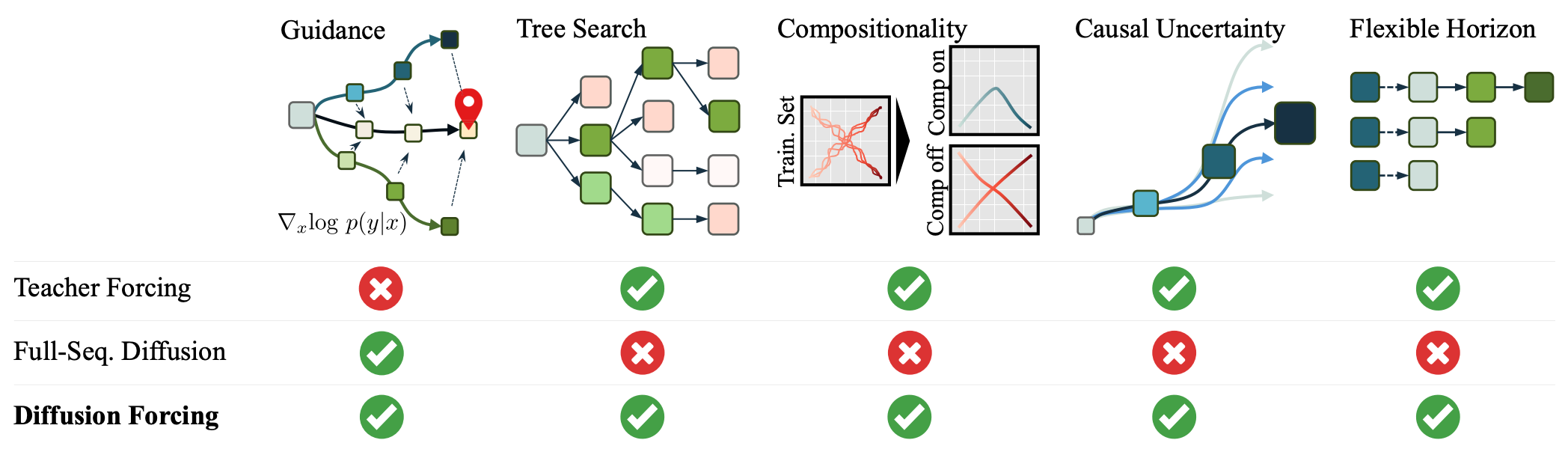
全序列扩散具有非因果、无掩码的架构，这限制了它只能对完整序列进行采样，而无法进行可变长度的生成。

这不仅限制了引导能力，也限制了 subsequence（子序列）级别的生成。

将全序列扩散与下一 token 模型结合的天真尝试会导致糟糕的生成效果，其原因在于它未能建模这样一个事实：早期 token 中的小不确定性会在后续 token 中导致巨大的不确定性。

3 方法（Method） Link to 3 方法（Method）

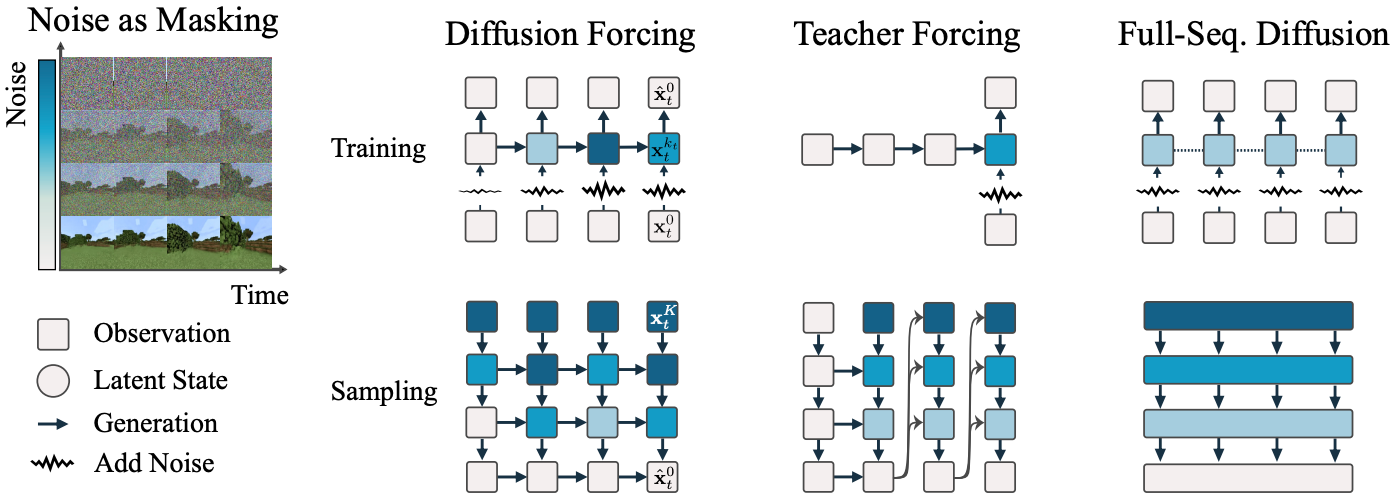
3.1 将加噪视为部分掩码（Noising as partial masking） Link to 3.1 将加噪视为部分掩码（Noising as partial masking）

回顾 masking（掩码）指的是遮蔽数据的某些子集，例如图像的部分区域或序列中的时间步，并训练模型恢复未被遮蔽的部分。

一般来说，我们可以将任意 token 集合（无论是否是序列）视为按时间索引 $t$ 排序的一组元素。

使用 teacher forcing 训练下一 token 预测模型可以被解释为：在时间 $t$ 对 token $\mathbf{x}_t$ 进行“掩码”，并根据过去的 $\mathbf{x}_{1:t-1}$ 来预测该 token。

针对序列，我们将此类做法称为：沿时间轴的掩码（masking along the time axis）。

我们也可以将全序列前向扩散过程，即逐渐对序列 $\mathbf{x}_{1:T}^0 \equiv \mathbf{x}_{1:T}$ 添加噪声，看作一种 部分掩码（partial masking），这里我们称之为：

沿噪声轴的掩码（masking along the noise axis）。

在经过 $K$ 步加噪后，$\mathbf{x}_{1:T}^K$（近似）成为无信息白噪声。

我们在两个掩码轴上建立了统一视角。

令 $\mathbf{x}_{1:T}$ 为长度为 $T$ 的 token 序列。如前所述，$\mathbf{x}_t^{k_t}$ 表示扩散过程中处于噪声等级 $k_t$ 的 token（公式见 (2.1)）。

此外，$\mathbf{x}_t^0 = \mathbf{x}$ 是未加噪 token，$\mathbf{x}_t^K$ 是白噪声 $\mathcal{N}(0,I)$。

因此，$(\mathbf{x}_t^{k_t})_{1\le t\le T}$ 是一个带噪序列，每个 token 具有不同噪声等级，可视为不同程度的部分掩码。

3.2 Diffusion Forcing：不同 token 使用不同噪声等级 Link to 3.2 Diffusion Forcing：不同 token 使用不同噪声等级

Diffusion Forcing 是一个训练与采样框架，用于处理任意序列长度的带噪 token 序列 $(\mathbf{x}_t^{k_t})_{1\le t\le T}$，其关键在于：

每个 token 的噪声等级 $k_t$ 可以随时间步变化。

本文关注时间序列数据，因此将 DF 实例化为具有因果结构的方法：

Causal Diffusion Forcing（CDF） Link to

为简单起见，我们使用：

• 一个 vanilla RNN（循环神经网络）

（Transformer 实现见附录 B.1。）

RNN 的隐藏状态 $\mathbf{z}_t$ 表示过去 token 的影响，更新如下：

当输入带噪 token $\mathbf{x}_t^{k_t}$ 时：

• 若 $k_t = 0$，对应贝叶斯滤波的“后验更新”
• 若 $k_t = K$，对应贝叶斯滤波的“先验更新”

给定 $\mathbf{z}_t$，观测模型：

预测干净 token $\mathbf{x}_t$。

训练（Training） Link to

动态模型：

与观测模型：

组合构成 RNN 单元。

模型根据 $\mathbf{z}_{t-1}$ 与带噪 token $\mathbf{x}_t^{k_t}$ 预测：

并通过重参数化生成噪声 $\epsilon_t$。

训练目标为标准扩散损失的时间序列版本：

其中：

• $k_{1:T} \sim [K]^T$
• $\mathbf{x}_{1:T}$ 来自训练集
• $\epsilon_t \sim \mathcal{N}(0, \sigma_k^2 I)$

定理 3.1（非正式） Link to

Diffusion Forcing 的训练过程（算法 1）优化一个 ELBO 的重加权形式，期望取于：

• 所有噪声序列 $k_{1:T} \sim [K]^T$
• 所有带噪 token $\mathbf{x}_t^{k_t}$

在适当条件下，目标 (3.1) 也最大化所有训练序列子序列的 ELBO。

如果 $k_t$ 只可能取 $0$ 或 $K$，DF 可以学习到：

• 任意 token 被遮蔽后的条件分布
• 即所有训练序列的所有子序列的分布

采样（Sampling） Link to

DF 的采样由一个二维噪声调度矩阵定义：

• 列对应时间步 $t$
• 行对应噪声更新阶段 $m$

$\mathcal{K}_{m,t}$ 表示第 $m$ 行中第 $t$ 个 token 的目标噪声等级。

采样步骤：

1. 初始化 $\mathbf{x}_{1:T}$ 为白噪声（等级 $K$）。
2. 按行从上到下遍历矩阵 $\mathcal{K}$。
3. 每一行中按列从左到右去噪，使 token 匹配 $\mathcal{K}_{m,t}$。

最终（$m=0$ 行）得到干净序列（噪声等级 0）。

不同的 $\mathcal{K}$ 产生不同采样行为，无需重新训练模型。

3.3 序列生成中的新能力（New Capabilities in Sequence Generation） Link to 3.3 序列生成中的新能力（New Capabilities in Sequence Generation）

下面解释这一灵活采样框架带来的新能力。

稳定自回归生成 Link to

在高维连续序列（如视频）中，传统自回归模型在超出训练长度时会发散。
DF 使用轻噪声 token 更新隐藏状态，使长序列生成稳定。

实验见 Sec. 4.1，进一步直觉见附录 B.4。

保持未来不确定性 Link to

从白噪声序列开始：

可以：

• 完全去噪第一 token： $[\mathbf{x}_1^0, \mathbf{x}_2^K, \mathbf{x}_3^K]^\top$
• 部分去噪第二 token： $[\mathbf{x}_1^0, \mathbf{x}_2^{K/2}, \mathbf{x}_3^K]^\top$
• 最终完全去噪所有 token： $[\mathbf{x}_1^0, \mathbf{x}_2^0, \mathbf{x}_3^0]^\top$

这种“zig-zag（之字形）”方式编码：

• 近未来更确定
• 远未来更不确定

从而提高引导效果。

长期引导（Long-horizon Guidance） Link to

算法 2 第 10 行允许对部分去噪的轨迹 $\mathbf{x}_{1:T}$ 添加引导。
由于未来 token 依赖过去 token，引导梯度可从未来反向传播到过去。

DF 的优势在于：

不完全去噪未来 token 的情况下，
可以影响过去 token 的采样，
实现长期引导且保持因果性。

实现细节见附录 B.3。

实验（Sec. 4.2）显示 DF 的规划性能远优于全序列扩散。

3.4 用于灵活序列决策的 Diffusion Forcing Link to 3.4 用于灵活序列决策的 Diffusion Forcing

DF 提供的能力激发我们提出新框架：

序列决策（Sequential Decision Making, SDM） Link to

应用领域包括机器人与自动化。

考虑马尔可夫决策过程：

• 环境动态
  $p(s_{t+1}\mid s_t, a_t)$
• 观测
  $p(o_t\mid s_t)$
• 奖励
  $r_t = r(s_t, a_t)$

目标是学习策略 $\pi(a_t\mid o_{1:t})$ 最大化期望累计奖励。

定义 token：

轨迹为 $\mathbf{x}_{1:T}$。

训练如算法 1。
在时间步 $t$：

1. 得到隐藏状态 $\mathbf{z}_{t-1}$
2. 使用算法 2 预测前瞻序列
   $\hat{\mathbf{x}}_{t:t+H}$

执行 $\hat a_t$ 后，得到奖励 $r_t$ 和观测 $o_{t+1}$，更新 token 和隐藏状态：

DF 既能作为 policy 又能作为 planner。

灵活规划范围（Flexible planning horizon） Link to

DF 的优势：

• 可用于不同规划范围的任务（短或长）
• 不需重新训练模型
• 可通过改变前瞻窗口 $H$ 实现不同策略/规划行为

全序列扩散（如 Diffuser [37]）无法实现这一点。

灵活奖励引导（Flexible reward guidance） Link to

DF 可使用任意奖励替代 $\log c$ 进行引导，包括：

• 全轨迹奖励 $\sum_{t=1}^T r_t$
• 前瞻奖励 $\sum_{t'=t}^{t+H} r_{t'}$
• 稀疏目标奖励 $-\lVert o_T - g\rVert^2$

这是逐时间步策略无法实现的。

Monte Carlo Guidance（MCG）与未来不确定性 Link to

CDF 允许基于整个未来分布 $\mathbf{x}_{t+1:T}$ 指导当前 token $\mathbf{x}_t^{k_t}$。

方法：

• 不用单一样本估计梯度
• 取未来多样本平均梯度
• 得到更稳健的引导

称为 Monte Carlo Guidance (MCG)。

类似 shooting 方法 MPPI [64]，但更灵活。

MCG 在未来 token 噪声大的调度下（如 Sec. 3.3 的 zig-zag 调度）效果更佳。

理论支撑见附录 D.5。